食い延ばし

食い延ばしという技術がある
愚形複合ターツから鳴いて待ちを良くするアレである
ex. 34568から25チーでカン4から47待ちに変える、みたいな
ある程度麻雀に慣れてくると自分がなんの牌で食い延ばすべきかは分かってくるものである
重要なのは他家の食い延ばしを見破ることである
これについてはググってもそんなにヒットしないようなので食い延ばした時の捨て牌から待ちを読む公式的なものを備忘録的に記しておく
理想は公式として覚えずに相手の手牌を想像して読むことだがいちいちそんなことに頭のリソースを割くほど余裕のないことが多いのでやはり機械的に覚えてしまうことが楽ではある
ただ他の捨て牌読みにも言えることだが一点読みは基本的に不可能なので他に安牌が無い時の参考までにとどめておいたほうがいいだろう

というわけで以下は愚形含みの5枚形（？）で食い延ばした時の公式である

①　鳴いた牌のスジを切ったらその裏スジが待ち
例チー打待ち
25で鳴いてスジの8が出たらその裏スジの47があたりになっているパティーン
これは比較的覚えやすいか
あえて名付けるならカンチャン整理型その１ってところか
以下全パティーン
元の形　喰い取り牌　切る牌　待ち（裏スジ）
12346　　3　　　　　 6　　　25
23457　　14　　　　　7　　　36
34568　　25　　　　　8　　　47
45679　　36　　　　　9　　　58
13456　　47　　　　　1　　　25
24567　　58　　　　　2　　　36
35678　　69　　　　　3　　　47
46789　　7　　　　　 4　　　58
ちなみにこの形では5は切られない

②の１　鳴いた牌の±4を切ったらそのスジが待ち
例チー打待ち
±4と書くとわかりづらいけど要は喰いとった牌と切った牌の間に順子ができる場合ってこと
元の形　喰い取り牌　切る牌　待ち（裏スジ）
12346　　2　　　　　6　　　3
23457　　3　　　　　7　　　14
34568　　4　　　　　8　　　25
45679　　5　　　　　9　　　36
13456　　5　　　　　1　　　47
24567　　6　　　　　2　　　58
35678　　7　　　　　3　　　69
46789　　8　　　　　4　　　7
スジのうち外側か内側かについては、そもそも食い延ばしが上家が捨てた牌を手元に2枚温存する手段であるので喰いとった牌で両面を構成するほうのスジと考えるとわかりやすいか

②の２　鳴いた牌の±4を切ったらその跨ぎスジが待ち

③

④　5切ったら鳴いたのと別のスジ待ち
（147チーして打5なら待ち369、369チーして打5なら147と大まかにおぼえればいい。。。のか？）

疲れた

シャドバでリセマラすべきか

最近はまってるシャドウバースというカードゲーム
他のスマホゲーよろしくリセマラを行うことでよりレア度の高いカードを引くことができる
では実際リセマラはするべきであるか？
回答をするならば”嫌になるのでリセマラすべきではない”
そもそも手慰みでゲームしてんのにいきなり単純労働を強いるのはあまりにマゾヒスティックではないか
だいたいシャドバはいらないカード砕いて自分の欲しいカードを生成するシステムがあるのでそこまで右手力は問われないし毎日ログインしてればログボとミッションでわりと引ける
それでもリセマラをしたい向きのためにどの程度の枚数レジェンドを引けばリセマラ成功といえるのかちょっと計算してみた

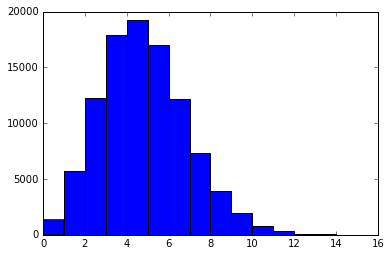
import matplotlib.pyplot as plt
import random
import collections as col

a = []
p = 1.5 #虹確率
pack = 36

def risemara(x):
    time = pack * 8
    for j in range(x):
        leg = 0
        for i in range(time):
            count = random.uniform(0,100)
            if count < p:
                leg += 1
        a.append(leg)

risemara(100000) #リセマラ回数

plt.hist(a,bins=max(a))
print(pack,"パックを",x,"回リセマラした場合に引くレジェンド（確率",p,"）の枚数")
aaa = col.Counter(a)
for key ,value in sorted(aaa.items()):
    print(key,"枚",value,"回、その確率は",(value/x)*100,"%")

36 パックを 100000 回リセマラした場合に引くレジェンド（確率 1.5 ）の枚数
0 枚 1348 回、その確率は 1.348 %
1 枚 5728 回、その確率は 5.728 %
2 枚 12214 回、その確率は 12.214 %
3 枚 17905 回、その確率は 17.904999999999998 %
4 枚 19260 回、その確率は 19.259999999999998 %
5 枚 17001 回、その確率は 17.000999999999998 %
6 枚 12158 回、その確率は 12.158 %
7 枚 7327 回、その確率は 7.327 %
8 枚 3913 回、その確率は 3.913 %
9 枚 1912 回、その確率は 1.9120000000000001 %
10 枚 785 回、その確率は 0.7849999999999999 %
11 枚 299 回、その確率は 0.299 %
12 枚 102 回、その確率は 0.10200000000000001 %
13 枚 32 回、その確率は 0.032 %
14 枚 12 回、その確率は 0.012 %
15 枚 4 回、その確率は 0.004 %

現在インストール直後のボーナスで36パック引けるようだが、それで7~9枚引ければ成功といえるのではないか

ところでこれって典型的なベルヌーイ試行である
というわけでnumpyのbinomial関数を使ってみる

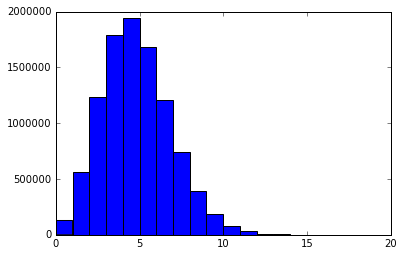
import matplotlib.pyplot as plt
import numpy as np
import collections as col

#numpy.random.binomialを使った場合
p = 1.5/100 #レジェンド
pack = 36
time = pack*8
x = 10000000 #試行回数
leg = np.random.binomial(time,p,x) #リストとなる
legdict = col.Counter(leg)

plt.hist(leg,bins=max(leg)) #なぜかデフォでbins=10

print(pack,"パックを",x,"回リセマラした場合に引くレジェンド（確率",p,"）の枚数")
for key ,value in sorted(legdict.items()):
    print(key,"枚",value,"回、その確率は",(value/x)*100,"%")

36 パックを 10000000 回リセマラした場合に引くレジェンド（確率 0.015 ）の枚数
0 枚 128278 回、その確率は 1.28278 %
1 枚 564045 回、その確率は 5.64045 %
2 枚 1234020 回、その確率は 12.3402 %
3 枚 1792282 回、その確率は 17.92282 %
4 枚 1943714 回、その確率は 19.43714 %
5 枚 1680494 回、その確率は 16.80494 %
6 枚 1207038 回、その確率は 12.07038 %
7 枚 739904 回、その確率は 7.399039999999999 %
8 枚 396402 回、その確率は 3.96402 %
9 枚 187852 回、その確率は 1.8785199999999997 %
10 枚 79711 回、その確率は 0.79711 %
11 枚 30445 回、その確率は 0.30445 %
12 枚 10814 回、その確率は 0.10814 %
13 枚 3543 回、その確率は 0.035429999999999996 %
14 枚 1074 回、その確率は 0.01074 %
15 枚 287 回、その確率は 0.00287 %
16 枚 73 回、その確率は 0.0007300000000000001 %
17 枚 17 回、その確率は 0.00017 %
18 枚 5 回、その確率は 4.9999999999999996e-05 %
19 枚 1 回、その確率は 9.999999999999999e-06 %
20 枚 1 回、その確率は 9.999999999999999e-06 %

最初かいたコードとおよそ似たような結果になったので満足
ところで標準ライブラリのrandomを使うと100万回試行で軽食が取れる程度には時間食うのに、ふたつめのコードで使ったnumpyのやつだと1000万回回してもものの数秒で終わるのはどういう理由からなのだろう

kiwami high low攻略

kiwami high lowというフリゲがあって、まあ普通のハイロウゲームなんだけど、ちゃんと遊んだことなかったのでやってみるとコレが面白く、熱中してしまった、30分くらい

毎ゲームごとにプレイヤーがミスをすると、女の子（きわみちゃん？）相手にロシアンルーレットが始まり、運良く空発だと女の子が恐怖で失禁するのだが、この演出がなかなか良くて、酒のみながらプレイしてたのもあってとても興奮する　そして運が悪いと普通に死ぬ

以下は攻略というほどでもないが、PCに眠らせておくのもなんかアレなので、ここに置いておく

 

---

そもそものルール、ハイローに成功するたびに所持金が2倍になっていき最終的に1億円を達成していれば勝利

ドロー又はパスの場合所持金は不変

また20億円を達成したら別endとなる

数字を外すとロシアンルーレットが始まり確率で死ぬ

ハイローを終えても1億に満たないとbad end

ハイローの代わりにセイムを成功させると所持金が10倍になる

 

35ターンあるのでそれまでに1億円を達成しないといけない

成功するたび金額は2倍になるので、逆に言えば1億達成するために必要な成功回数は対数で計算できる

log2(1億円)≒26.57 ：つまりセイムなしで1億円達成するためには27回正解する必要があり、ミスとパスを計8回まで許容できる

ミスの確率を考えれば現実的に3パスまでか

セイムなしで20億達成するなら?　log2(20億)≒30.89なので31回 は正解しないといけない　つまり4ミスまで、厳しい？

5ミスで確定射殺

 

セイムはいつ出してもいい、なら初手セイムを成功させるリセマラしたほうが効率いい

一発目にセイムになる確率は3/35≒0.0857つまり8.6%

2連セイムは無理...（連続セイムは数字が続くのでセイム正解セイムを狙うとして、確かに金額達成という意味では楽になるが確率的にはかなり厳しい、リセマラするにしても時間の無駄

単純計算で2連セイムが0.86^2=0.73%　はい無理）

3正解より1セイムのほうが価値あり、つまり初手セイムを決めればわりと休める

 

リセマラして初手セイムを成功させるとして、それぞれの成功条件は

log2(1億円/10)≒23.25

log2(20億円/10)≒27.57

つまり1億達成したいなら初手セイム成功のリセマラさえすればパスもしくはハイローの失敗を計10回まで、

20億達成したいなら、初手セイム成功のリセマラさえすればパスもしくはハイローの失敗を計6回まで繰り返せる

20億達成したいなら、5を全部パスなんて悠長なことはやってられない

 

結論→初回パスリセマラしろ、成功したらミスとパスの数を数えつつ後は運否天賦