iphoneで小説を読む
要約:青空文庫のように整形されてない文章、例えばネットに落ちてる怪文書をiphoneで読みたいという場合、i文庫sを購入しましょう
i文庫sは最高
アプリは今のとこkinoppyが読みやすい
ただzipを読み込むとたまに死ぬ
生txtよりもpdfにしといたほうが何かと読みやすいという点では勝る
ではどのように変換するか、google driveのdocsを使う
txtをコピペで読み込み、設定は余白1.5~2cmあたり、用紙サイズlegal、フォントメイリオで文字サイズ20か
これでpdf出力できるので完璧
kinoppyマジでzip読み込むとたまに死んで全部やり直し問題がウザすぎて250円でi文庫s導入
これがまた使いやすくて最高 生txt読みやすいしpdf余白調製あるしついでに青空読めるしもうこれでよい
● 特殊記号使われると表記崩れる問題
→❤が機種依存なので♥に置換、あと”ゔ〰〰〰〰〰〰❤❤❤❤”も機種依存だけどそこまで深刻ではないので放置
→utf-8で保存してオールおけー
●i文庫ではzip読み込めん問題
→pic2pdfでpdf化してオールおけー
→でもなぜかfile explorer でftp転送するとpdfがバグる
→sendanywherで送ることで解決 マジでわからん
熾天使をマリガン時デッキ戻しした場合にその後引く確率
タイトル通り
エイラと違って8Tまで持ってても仕方ないので基本戻す
import random as rd import matplotlib.pyplot as plt import collections as col target = 3 #セラフ others = 40 - target m = 2 #マリガン枚数 time = 1000000 #試行回数 def mulligan(): """熾天使をマリガンで戻した場合、何ターンまでに引いてるか。todo キャントリやプリプリの考慮""" x = [] #ターゲットが来たターンから成るリスト。0は初手orマリガンで来た場合、それ以外は来たターン。後攻は-1ターンして考える for j in range(time): deck = [] hand = [] for i in range(target): deck.append("t") for i in range(others): deck.append("o") rd.shuffle(deck) #デッキ作成&まぜまぜ完了 for i in range(3): hand.append(deck.pop()) #マリガン前初手引き tnum = col.Counter(hand) for i in range(tnum["t"]): #初手熾天使あるならdeckに戻して hand.remove("t") deck.append("t") rd.shuffle(deck) for i in range(tnum["t"]): hand.append(deck.pop()) #戻した数だけカード引く if "t" in hand: x.append(0) #初手熾天使が有って、それマリガンで戻してもまた来た場合 continue for i in range(37): #マリガンしてターゲットが無い場合 if deck.pop() == "t": x.append(i+1) break plt.hist(x,bins=max(x)) aaa = col.Counter(x) totalprb = 0 for i in range(16): prb = (aaa[i]/time)*100 totalprb += prb print(i,"ターン目までにターゲットを引いている確率",totalprb,"%") mulligan() print("マリガン",m,"枚") print(time,"回試行")
0 ターン目までにターゲットを引いている確率 1.7543 %
1 ターン目までにターゲットを引いている確率 9.7392 %
2 ターン目までにターゲットを引いている確率 17.2676 %
3 ターン目までにターゲットを引いている確率 24.321400000000004 %
4 ターン目までにターゲットを引いている確率 31.010200000000005 %
5 ターン目までにターゲットを引いている確率 37.276900000000005 %
6 ターン目までにターゲットを引いている確率 43.1884 %
7 ターン目までにターゲットを引いている確率 48.6363 %
8 ターン目までにターゲットを引いている確率 53.756099999999996 %
9 ターン目までにターゲットを引いている確率 58.5391 %
10 ターン目までにターゲットを引いている確率 62.986799999999995 %
11 ターン目までにターゲットを引いている確率 67.0842 %
12 ターン目までにターゲットを引いている確率 70.90419999999999 %
13 ターン目までにターゲットを引いている確率 74.40259999999999 %
14 ターン目までにターゲットを引いている確率 77.6117 %
15 ターン目までにターゲットを引いている確率 80.5283 %
マリガン 2 枚 熾天使3枚
1000000 回試行
0 ターン目までにターゲットを引いている確率 0.7992000000000001 %
1 ターン目までにターゲットを引いている確率 6.1516 %
2 ターン目までにターゲットを引いている確率 11.3437 %
3 ターン目までにターゲットを引いている確率 16.4056 %
4 ターン目までにターゲットを引いている確率 21.298000000000002 %
5 ターン目までにターゲットを引いている確率 26.0973 %
6 ターン目までにターゲットを引いている確率 30.713900000000002 %
7 ターン目までにターゲットを引いている確率 35.1751 %
8 ターン目までにターゲットを引いている確率 39.5017 %
9 ターン目までにターゲットを引いている確率 43.6909 %
10 ターン目までにターゲットを引いている確率 47.727599999999995 %
11 ターン目までにターゲットを引いている確率 51.61619999999999 %
12 ターン目までにターゲットを引いている確率 55.34459999999999 %
13 ターン目までにターゲットを引いている確率 58.85809999999999 %
14 ターン目までにターゲットを引いている確率 62.27709999999999 %
15 ターン目までにターゲットを引いている確率 65.5645 %
マリガン 2 枚 熾天使2枚
1000000 回試行
実際はキャントリ持ちやプリプリがあるのでもうちょっと早くなる
キャントリについては積んでる枚数多いだろうしターンを読み替えるだけで近似できそうな気はするけどプリプリの影響はでかいのでそういうのも考えないといけない、そのうちやる
マリガンした時に目的のカードが第nターンまでに手にある確率
例えば3積みしたカードをnターン目までに引く確率は何%か、みたいなちょっと混んだ確率を計算するとき、厳密に確率計算するよりとりあえずコード書いてシミュレーションしてみたほうがよっぽど都合の良い場合がある
というわけで3積みしたエイラや御旗や超越やらをマリガンした場合に引いてくる確率を計算してみた
import random as rd import matplotlib.pyplot as plt import collections as col target = 3 #セラフ others = 40 - target m = 3 #マリガン枚数 time = 1000000 #試行回数 def mulligan(): x = [] #ターゲットが来たターンから成るリスト。0は初手orマリガンで来た場合、それ以外は来たターン。後攻は-1ターンして考える for j in range(time): deck = [] hand = [] for i in range(target): deck.append("t") for i in range(others): deck.append("o") rd.shuffle(deck) #デッキ作成&まぜまぜ完了 for i in range(3): hand.append(deck.pop()) #マリガン前初手引き if "t" in hand: x.append(0) #マリガン前に来たら終了 continue else: #マリガンしても来なかったら for i in range(m): deck.append(hand.pop()) rd.shuffle(deck) for i in range(m): hand.append(deck.pop()) if "t" in hand: x.append(0) continue #マリガンして来たら終了 rd.shuffle(deck) for k in range(37): #マリガンしてもターゲットが無い場合 aaa = deck.pop() if aaa == "t": x.append(k+1) break # print("deck",deck,len(deck)) # print("hand",hand,len(hand)) # print("x",x,len(x)) plt.hist(x,bins=max(x)) aaa = col.Counter(x) ppp = 0 for i in range(21): p = (aaa[i]/time)*100 ppp += p print(i,"ターン目にターゲットを引いている確率",ppp,"%") mulligan() print(time,"回試行") print("マリガン",m,"枚")
これをマリガンの枚数別に回してみる
上からノーチェンジ、1枚2枚フルマリガン
後攻は1T目2枚引きなので-1ターン考慮すること
0 ターン目にターゲットを引いている確率 21.3183 %
1 ターン目にターゲットを引いている確率 27.6999 %
2 ターン目にターゲットを引いている確率 33.7504 %
3 ターン目にターゲットを引いている確率 39.4381 %
4 ターン目にターゲットを引いている確率 44.790099999999995 %
5 ターン目にターゲットを引いている確率 49.821099999999994 %
6 ターン目にターゲットを引いている確率 54.517999999999994 %
7 ターン目にターゲットを引いている確率 58.94689999999999 %
8 ターン目にターゲットを引いている確率 63.048199999999994 %
9 ターン目にターゲットを引いている確率 66.8643 %
10 ターン目にターゲットを引いている確率 70.4036 %
11 ターン目にターゲットを引いている確率 73.6943 %
12 ターン目にターゲットを引いている確率 76.7449 %
13 ターン目にターゲットを引いている確率 79.52720000000001 %
14 ターン目にターゲットを引いている確率 82.09120000000001 %
15 ターン目にターゲットを引いている確率 84.42180000000002 %
16 ターン目にターゲットを引いている確率 86.53670000000002 %
17 ターン目にターゲットを引いている確率 88.44090000000003 %
18 ターン目にターゲットを引いている確率 90.16450000000003 %
19 ターン目にターゲットを引いている確率 91.72060000000003 %
20 ターン目にターゲットを引いている確率 93.09680000000003 %
1000000 回試行
マリガン 0 枚
0 ターン目にターゲットを引いている確率 27.693099999999998 %
1 ターン目にターゲットを引いている確率 33.5411 %
2 ターン目にターゲットを引いている確率 39.0525 %
3 ターン目にターゲットを引いている確率 44.2825 %
4 ターン目にターゲットを引いている確率 49.2106 %
5 ターン目にターゲットを引いている確率 53.8245 %
6 ターン目にターゲットを引いている確率 58.1519 %
7 ターン目にターゲットを引いている確率 62.201499999999996 %
8 ターン目にターゲットを引いている確率 66.0148 %
9 ターン目にターゲットを引いている確率 69.50269999999999 %
10 ターン目にターゲットを引いている確率 72.7652 %
11 ターン目にターゲットを引いている確率 75.8128 %
12 ターン目にターゲットを引いている確率 78.5983 %
13 ターン目にターゲットを引いている確率 81.172 %
14 ターン目にターゲットを引いている確率 83.5312 %
15 ターン目にターゲットを引いている確率 85.6756 %
16 ターン目にターゲットを引いている確率 87.6478 %
17 ターン目にターゲットを引いている確率 89.43690000000001 %
18 ターン目にターゲットを引いている確率 91.03460000000001 %
19 ターン目にターゲットを引いている確率 92.46020000000001 %
20 ターン目にターゲットを引いている確率 93.72140000000002 %
1000000 回試行
マリガン 1 枚
0 ターン目にターゲットを引いている確率 33.1351 %
1 ターン目にターゲットを引いている確率 38.5676 %
2 ターン目にターゲットを引いている確率 43.6727 %
3 ターン目にターゲットを引いている確率 48.5297 %
4 ターン目にターゲットを引いている確率 53.0668 %
5 ターン目にターゲットを引いている確率 57.3196 %
6 ターン目にターゲットを引いている確率 61.3138 %
7 ターン目にターゲットを引いている確率 65.0617 %
8 ターン目にターゲットを引いている確率 68.5632 %
9 ターン目にターゲットを引いている確率 71.7999 %
10 ターン目にターゲットを引いている確率 74.81559999999999 %
11 ターン目にターゲットを引いている確率 77.64699999999999 %
12 ターン目にターゲットを引いている確率 80.22789999999999 %
13 ターン目にターゲットを引いている確率 82.58359999999999 %
14 ターン目にターゲットを引いている確率 84.7405 %
15 ターン目にターゲットを引いている確率 86.73729999999999 %
16 ターン目にターゲットを引いている確率 88.56429999999999 %
17 ターン目にターゲットを引いている確率 90.20169999999999 %
18 ターン目にターゲットを引いている確率 91.68749999999999 %
19 ターン目にターゲットを引いている確率 92.97989999999999 %
20 ターン目にターゲットを引いている確率 94.14999999999999 %
1000000 回試行
マリガン 2 枚
0 ターン目にターゲットを引いている確率 38.209900000000005 %
1 ターン目にターゲットを引いている確率 43.217400000000005 %
2 ターン目にターゲットを引いている確率 47.984700000000004 %
3 ターン目にターゲットを引いている確率 52.41760000000001 %
4 ターン目にターゲットを引いている確率 56.569300000000005 %
5 ターン目にターゲットを引いている確率 60.4986 %
6 ターン目にターゲットを引いている確率 64.1774 %
7 ターン目にターゲットを引いている確率 67.63210000000001 %
8 ターン目にターゲットを引いている確率 70.89260000000002 %
9 ターン目にターゲットを引いている確率 73.89020000000002 %
10 ターン目にターゲットを引いている確率 76.67410000000002 %
11 ターン目にターゲットを引いている確率 79.24760000000002 %
12 ターン目にターゲットを引いている確率 81.62980000000002 %
13 ターン目にターゲットを引いている確率 83.83390000000001 %
14 ターン目にターゲットを引いている確率 85.85800000000002 %
15 ターン目にターゲットを引いている確率 87.72270000000002 %
16 ターン目にターゲットを引いている確率 89.40250000000002 %
17 ターン目にターゲットを引いている確率 90.90200000000002 %
18 ターン目にターゲットを引いている確率 92.26930000000002 %
19 ターン目にターゲットを引いている確率 93.48920000000001 %
20 ターン目にターゲットを引いている確率 94.5588 %
1000000 回試行
マリガン 3 枚
というわけでフルマリガンすると1T目には4割方手に入っているという結果に
正直想像以上に高いというか、実際フルマリガンすることも稀なのでこれで妥当という感じはする
matplotlibで二項分布を表示する(だけ)
先の記事で書いたコードだけどnumpy.random.binomial()で実際にサンプリングした数字からなるリストを作ってそっからヒストグラムつくるみたいなよく考えたら(よく考えなくても)頭悪いことしてたの今更気づいて、自分で単純なベルヌーイ試行だっつってんだからそのまま二項分布のグラフ書けばいいじゃねえかと思って書いた
range(x)が0から始まるリストを返すのにだけ気をつけて書くとこんな感じ
import matplotlib.pyplot as plt import scipy.misc as scm #組合せ計算用 p = 1.5/100 #レジェンド pack = 50 time = pack*8 def unko(): aaa = [] for j in range(time-1): elm = scm.comb(time,j) * (p**(j)) * ((1-p)**(time-j)) aaa.append(elm) print(aaa,sum(aaa)) #表示される数は*100すると%表示になる。そっちのが見やすいか? plt.plot(aaa) unko()
[0.014428036055035228, 0.043833398877860821, 0.088556816007048775, 0.13384665972638971, (以下略)
1.0
オッ
import matplotlib.pyplot as plt import scipy.misc as scm #組合せ計算用 p = 1.5/100 #レジェンド pack = 50 time = pack*8 def unko(): aaa = [] for j in range(time-1): elm = scm.comb(time,j) * (p**(j)) * ((1-p)**(time-j)) aaa.append(elm) print(aaa,sum(aaa)) #表示される数は*100すると%表示になる。そっちのが見やすいか? plt.plot(aaa) plt.xlim([0,20]) #x軸を0から20までに絞る unko()
<
ちなみにこの50パックという数字は9800円課金してそのままガチャ回した時の確率である
この分布の平均と標準偏差はそれぞれ
m = time*p s = (time*p*(1-p))**(1/2) print(m-s,m+s)
3.5689508437713564 8.431049156228644
なので諭吉放りこむとおよそ3回に2回は3~8枚引ける計算になる
これやっぱリセマラすべきなんじゃ…
pythonで解くソローモデル 初級編
経済学を勉強していくとソローsolowモデルというものに出会う
例えば学部で学ぶケインジアンのISLMなんかは静学分析といって当期だけの均衡を見るが、現実問題として投資すれば投資するだけ来期のGDPとか消費とかが伸びることは想像に難くない
雑に言うとそーゆー時間経過の影響も見ましょうよっていうのがソローモデルである
ところでいきなりいろいろ未知数とかパラメータもりこんで複雑な連立方程式を解こうとしても挫折するのでシンプルなモデルからやってみましょうよ、ついでに自力で計算するのも面倒なのでpythonで説いてみましょうねというのがこのエントリの趣旨である
ちなみに自分は大して勉強してない(なんせ留年してる)ので話半分に聞いておくと吉だ
変数は世に(というかモデルに)たくさんあるが、内生変数をYとKに絞れば(つまりいろんなパラメータとか人口Lとか技術水準Aとかを常に既知とすると)2つの方程式で古典派の成長理論を表すことができる
とりあえずこれを最もシンプルなソローモデルとでも呼んでみよう
前者は生産関数、後者は資本蓄積式である
繰り返すがここで未知数は各期のYとKのみ、便宜的にや
と表記しているがこれらはすべての期で一定、加えてα(資本分配率)やδ(資本減耗率)やs(貯蓄率)も一定とするとこれは0期のKの値だけ与えてやれば解ける
というわけで解いてみよう
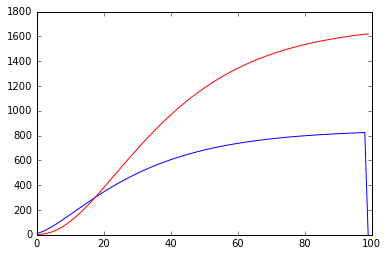
# -*- coding: utf-8 -*- import numpy as np import matplotlib.pyplot as plt t = 100 #何期までやるか Y = np.empty(t) K = np.empty(t) alpha = 0.6 #コブダグラス型の労働分配率あるいは資本分配率。数字は適当 delta = 0.1 #資本減耗率。こちらも適当 s = 0.2 #貯蓄率。適当 K[0] = 1 #単位は便宜的に万円ということで A = 10 #技術水準あるいは全要素生産性、今回は外生値。単位は知らん L = 30 #人口。単位は便宜的に万人で。 class Solow: """最もシンプルなソローモデル""" def __init__(self,Y,K): self.Y, self.K = Y,K def calc(self): for i in range(t-1): self.Y[i] = (self.K[i]**alpha) * ((A*L)**(1-alpha)) #コブダグラス型生産関数 self.K[i+1] = (1-delta)*self.K[i] + s*self.Y[i] #資本蓄積 obj = Solow(Y,K) ans = obj.calc() print(Y) plt.plot(Y,"blue") plt.plot(K,"red")
まあこんな感じであろうか
numpyのempty関数でYとKのt期分の空きリストを作っておいて、0期のKと各パラメータを外生的に与えてやり、あとは適当に方程式を与えてやれば解ける、みたいな
実行結果
runfile('C:/Users/a/Desktop/temp1.py', wdir='C:/Users/a/Desktop')
[ 9.79148362 18.38708522 29.40164841 42.40192563 56.99399415
(中略)
815.21230173 816.53530369 817.80614335 819.02684748 820.19936649
821.32557714 822.4072851 823.44622751 824.4440754 0. ]
グラフの赤線は資本Kの額、青線は所得Yの額である
数字は適当だが100期ちょい過ぎで均衡値に達するであろうことが見て取れる
こーゆーのなんて言うんだっけ、定差方程式?違ったらごめん
これがソローモデルの最低限な部分かな 普通はこれのAとKを
こんな感じに内生化する。(や
はそれぞれ技術進歩率、人口成長率である、念のため)
お察しの通りこのモデルには家計や企業の意思決定が介在していない(あと政府と海外部門も)
普通ソローモデルと呼ばれるものはここに企業の利潤最大化を盛り込んで資本蓄積させたものをいう(ハズ)
そうして組んだモデルはほっといてもそのうち均衡点に達するというのが教科書的な新古典派経済学の主張である(たぶん)
ついでに家計の効用最大化を盛り込むとラムゼーモデルになり、さらに失業と技術ショックをとりいれてRBC、硬直性や市場の不完全性などケインズ的な要素を取り入れてDSGEというようにいろんな現代的なモデルの骨子となっているので勉強しましょうという話
気が向いたら続きます
おわり
食い延ばし
食い延ばしという技術がある
愚形複合ターツから鳴いて待ちを良くするアレである
ex. 34568から25チーでカン4から47待ちに変える、みたいな
ある程度麻雀に慣れてくると自分がなんの牌で食い延ばすべきかは分かってくるものである
重要なのは他家の食い延ばしを見破ることである
これについてはググってもそんなにヒットしないようなので食い延ばした時の捨て牌から待ちを読む公式的なものを備忘録的に記しておく
理想は公式として覚えずに相手の手牌を想像して読むことだがいちいちそんなことに頭のリソースを割くほど余裕のないことが多いのでやはり機械的に覚えてしまうことが楽ではある
ただ他の捨て牌読みにも言えることだが一点読みは基本的に不可能なので他に安牌が無い時の参考までにとどめておいたほうがいいだろう
というわけで以下は愚形含みの5枚形(?)で食い延ばした時の公式である
① 鳴いた牌のスジを切ったらその裏スジが待ち
例![]()
![]()
![]()
![]()
![]() チー
チー![]()
![]() 打
打![]() 待ち
待ち![]()
![]()
25で鳴いてスジの8が出たらその裏スジの47があたりになっているパティーン
これは比較的覚えやすいか
あえて名付けるならカンチャン整理型その1ってところか
以下全パティーン
元の形 喰い取り牌 切る牌 待ち(裏スジ)
12346 3 6 25
23457 14 7 36
34568 25 8 47
45679 36 9 58
13456 47 1 25
24567 58 2 36
35678 69 3 47
46789 7 4 58
ちなみにこの形では5は切られない
②の1 鳴いた牌の±4を切ったらそのスジが待ち
例![]()
![]()
![]()
![]()
![]() チー
チー![]() 打
打![]() 待ち
待ち![]()
![]()
±4と書くとわかりづらいけど要は喰いとった牌と切った牌の間に順子ができる場合ってこと
元の形 喰い取り牌 切る牌 待ち(裏スジ)
12346 2 6 3
23457 3 7 14
34568 4 8 25
45679 5 9 36
13456 5 1 47
24567 6 2 58
35678 7 3 69
46789 8 4 7
スジのうち外側か内側かについては、そもそも食い延ばしが上家が捨てた牌を手元に2枚温存する手段であるので喰いとった牌で両面を構成するほうのスジと考えるとわかりやすいか
②の2 鳴いた牌の±4を切ったらその跨ぎスジが待ち
③
④ 5切ったら鳴いたのと別のスジ待ち
(147チーして打5なら待ち369、369チーして打5なら147と大まかにおぼえればいい。。。のか?)
疲れた
シャドバでリセマラすべきか
最近はまってるシャドウバースというカードゲーム
他のスマホゲーよろしくリセマラを行うことでよりレア度の高いカードを引くことができる
では実際リセマラはするべきであるか?
回答をするならば”嫌になるのでリセマラすべきではない”
そもそも手慰みでゲームしてんのにいきなり単純労働を強いるのはあまりにマゾヒスティックではないか
だいたいシャドバはいらないカード砕いて自分の欲しいカードを生成するシステムがあるのでそこまで右手力は問われないし毎日ログインしてればログボとミッションでわりと引ける
それでもリセマラをしたい向きのためにどの程度の枚数レジェンドを引けばリセマラ成功といえるのかちょっと計算してみた
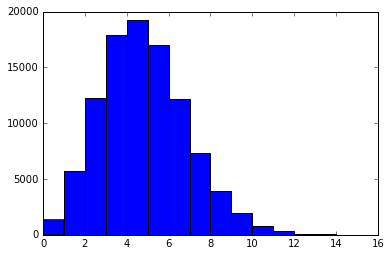
import matplotlib.pyplot as plt import random import collections as col a = [] p = 1.5 #虹確率 pack = 36 def risemara(x): time = pack * 8 for j in range(x): leg = 0 for i in range(time): count = random.uniform(0,100) if count < p: leg += 1 a.append(leg) risemara(100000) #リセマラ回数 plt.hist(a,bins=max(a)) print(pack,"パックを",x,"回リセマラした場合に引くレジェンド(確率",p,")の枚数") aaa = col.Counter(a) for key ,value in sorted(aaa.items()): print(key,"枚",value,"回、その確率は",(value/x)*100,"%")
36 パックを 100000 回リセマラした場合に引くレジェンド(確率 1.5 )の枚数
0 枚 1348 回、その確率は 1.348 %
1 枚 5728 回、その確率は 5.728 %
2 枚 12214 回、その確率は 12.214 %
3 枚 17905 回、その確率は 17.904999999999998 %
4 枚 19260 回、その確率は 19.259999999999998 %
5 枚 17001 回、その確率は 17.000999999999998 %
6 枚 12158 回、その確率は 12.158 %
7 枚 7327 回、その確率は 7.327 %
8 枚 3913 回、その確率は 3.913 %
9 枚 1912 回、その確率は 1.9120000000000001 %
10 枚 785 回、その確率は 0.7849999999999999 %
11 枚 299 回、その確率は 0.299 %
12 枚 102 回、その確率は 0.10200000000000001 %
13 枚 32 回、その確率は 0.032 %
14 枚 12 回、その確率は 0.012 %
15 枚 4 回、その確率は 0.004 %
現在インストール直後のボーナスで36パック引けるようだが、それで7~9枚引ければ成功といえるのではないか
ところでこれって典型的なベルヌーイ試行である
というわけでnumpyのbinomial関数を使ってみる
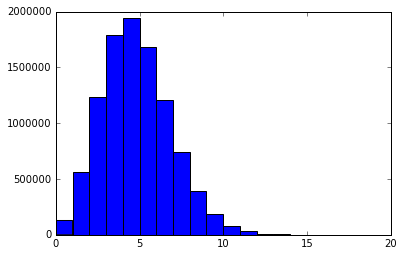
import matplotlib.pyplot as plt import numpy as np import collections as col #numpy.random.binomialを使った場合 p = 1.5/100 #レジェンド pack = 36 time = pack*8 x = 10000000 #試行回数 leg = np.random.binomial(time,p,x) #リストとなる legdict = col.Counter(leg) plt.hist(leg,bins=max(leg)) #なぜかデフォでbins=10 print(pack,"パックを",x,"回リセマラした場合に引くレジェンド(確率",p,")の枚数") for key ,value in sorted(legdict.items()): print(key,"枚",value,"回、その確率は",(value/x)*100,"%")
36 パックを 10000000 回リセマラした場合に引くレジェンド(確率 0.015 )の枚数
0 枚 128278 回、その確率は 1.28278 %
1 枚 564045 回、その確率は 5.64045 %
2 枚 1234020 回、その確率は 12.3402 %
3 枚 1792282 回、その確率は 17.92282 %
4 枚 1943714 回、その確率は 19.43714 %
5 枚 1680494 回、その確率は 16.80494 %
6 枚 1207038 回、その確率は 12.07038 %
7 枚 739904 回、その確率は 7.399039999999999 %
8 枚 396402 回、その確率は 3.96402 %
9 枚 187852 回、その確率は 1.8785199999999997 %
10 枚 79711 回、その確率は 0.79711 %
11 枚 30445 回、その確率は 0.30445 %
12 枚 10814 回、その確率は 0.10814 %
13 枚 3543 回、その確率は 0.035429999999999996 %
14 枚 1074 回、その確率は 0.01074 %
15 枚 287 回、その確率は 0.00287 %
16 枚 73 回、その確率は 0.0007300000000000001 %
17 枚 17 回、その確率は 0.00017 %
18 枚 5 回、その確率は 4.9999999999999996e-05 %
19 枚 1 回、その確率は 9.999999999999999e-06 %
20 枚 1 回、その確率は 9.999999999999999e-06 %
最初かいたコードとおよそ似たような結果になったので満足
ところで標準ライブラリのrandomを使うと100万回試行で軽食が取れる程度には時間食うのに、ふたつめのコードで使ったnumpyのやつだと1000万回回してもものの数秒で終わるのはどういう理由からなのだろう