pythonで解くソローモデル 初級編
経済学を勉強していくとソローsolowモデルというものに出会う
例えば学部で学ぶケインジアンのISLMなんかは静学分析といって当期だけの均衡を見るが、現実問題として投資すれば投資するだけ来期のGDPとか消費とかが伸びることは想像に難くない
雑に言うとそーゆー時間経過の影響も見ましょうよっていうのがソローモデルである
ところでいきなりいろいろ未知数とかパラメータもりこんで複雑な連立方程式を解こうとしても挫折するのでシンプルなモデルからやってみましょうよ、ついでに自力で計算するのも面倒なのでpythonで説いてみましょうねというのがこのエントリの趣旨である
ちなみに自分は大して勉強してない(なんせ留年してる)ので話半分に聞いておくと吉だ
変数は世に(というかモデルに)たくさんあるが、内生変数をYとKに絞れば(つまりいろんなパラメータとか人口Lとか技術水準Aとかを常に既知とすると)2つの方程式で古典派の成長理論を表すことができる
とりあえずこれを最もシンプルなソローモデルとでも呼んでみよう
前者は生産関数、後者は資本蓄積式である
繰り返すがここで未知数は各期のYとKのみ、便宜的にや
と表記しているがこれらはすべての期で一定、加えてα(資本分配率)やδ(資本減耗率)やs(貯蓄率)も一定とするとこれは0期のKの値だけ与えてやれば解ける
というわけで解いてみよう
# -*- coding: utf-8 -*- import numpy as np import matplotlib.pyplot as plt t = 100 #何期までやるか Y = np.empty(t) K = np.empty(t) alpha = 0.6 #コブダグラス型の労働分配率あるいは資本分配率。数字は適当 delta = 0.1 #資本減耗率。こちらも適当 s = 0.2 #貯蓄率。適当 K[0] = 1 #単位は便宜的に万円ということで A = 10 #技術水準あるいは全要素生産性、今回は外生値。単位は知らん L = 30 #人口。単位は便宜的に万人で。 class Solow: """最もシンプルなソローモデル""" def __init__(self,Y,K): self.Y, self.K = Y,K def calc(self): for i in range(t-1): self.Y[i] = (self.K[i]**alpha) * ((A*L)**(1-alpha)) #コブダグラス型生産関数 self.K[i+1] = (1-delta)*self.K[i] + s*self.Y[i] #資本蓄積 obj = Solow(Y,K) ans = obj.calc() print(Y) plt.plot(Y,"blue") plt.plot(K,"red")
まあこんな感じであろうか
numpyのempty関数でYとKのt期分の空きリストを作っておいて、0期のKと各パラメータを外生的に与えてやり、あとは適当に方程式を与えてやれば解ける、みたいな
実行結果
runfile('C:/Users/a/Desktop/temp1.py', wdir='C:/Users/a/Desktop')
[ 9.79148362 18.38708522 29.40164841 42.40192563 56.99399415
(中略)
815.21230173 816.53530369 817.80614335 819.02684748 820.19936649
821.32557714 822.4072851 823.44622751 824.4440754 0. ]
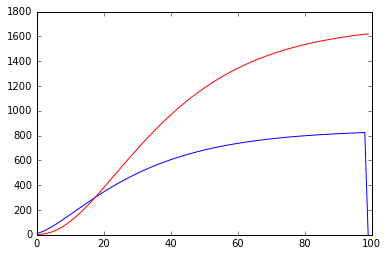
グラフの赤線は資本Kの額、青線は所得Yの額である
数字は適当だが100期ちょい過ぎで均衡値に達するであろうことが見て取れる
こーゆーのなんて言うんだっけ、定差方程式?違ったらごめん
これがソローモデルの最低限な部分かな 普通はこれのAとKを
こんな感じに内生化する。(や
はそれぞれ技術進歩率、人口成長率である、念のため)
お察しの通りこのモデルには家計や企業の意思決定が介在していない(あと政府と海外部門も)
普通ソローモデルと呼ばれるものはここに企業の利潤最大化を盛り込んで資本蓄積させたものをいう(ハズ)
そうして組んだモデルはほっといてもそのうち均衡点に達するというのが教科書的な新古典派経済学の主張である(たぶん)
ついでに家計の効用最大化を盛り込むとラムゼーモデルになり、さらに失業と技術ショックをとりいれてRBC、硬直性や市場の不完全性などケインズ的な要素を取り入れてDSGEというようにいろんな現代的なモデルの骨子となっているので勉強しましょうという話
気が向いたら続きます
おわり